3860번: 할로윈 묘지
오늘은 할로윈이다. 상근이와 친구들은 할로윈을 기념하기 위해 묘지를 방문했다. 상근이와 친구들은 한 명씩 묘지로 들어가고, 혼자서 묘지의 출구를 찾아야 한다. 이제, 상근이의 차례가 돌아
www.acmicpc.net
문제 요약
할로윈에 할짓이 없는지 묘지 탐험을 하는 상근이. 입구로 들어가서 출구로 최대한 빨리 나오는 것이 목표.
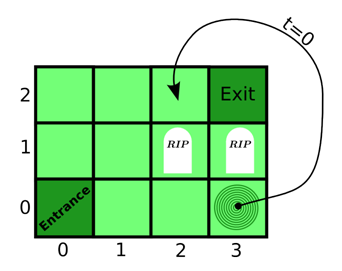
묘지는 W × H 크기의 그리드 형태. 묘지의 입구는 (0, 0)이고, 출구는 (W-1, H-1)이다.
상근이는 최대한 빨리 묘지를 나가려고 한다. 그리고 상근이는 이동하던 도중 출구에 도달하면 그 즉시 묘지를 빠져나간다.
상근이는 현재 있는 칸과 동, 서, 남, 북으로 인접한 칸으로 이동할 수 있다.
각 칸은 잔디, 묘비, 또는 귀신 구멍이다.
- 묘비는 매우 높기 때문에, 묘비가 있는 칸으로는 이동할 수 없다.
- 귀신 구멍이 있는 칸으로 이동하면, 특정 시간이 지난 후에 묘지의 다른 곳에서 상근이가 나타나게 된다. 시간은 귀신 구멍마다 다르며, 양수, 음수, 0 중 하나이다.
- 잔디가 있는 칸으로는 자유롭게 이동할 수 있다. 인접한 칸으로 이동할 때 걸리는 시간은 1이다.
상근이는 묘지를 빨리 나가기 위해 귀신 구멍도 이용할 것이다. 묘지를 나갈 수 없는 경우나, 계속해서 과거로 이동하는 경우가 존재할 수도 있다.
입력
여러 개의 테스트 케이스로 이루어져 있다.
각 테스트 케이스의 첫째 줄에는 묘지의 너비 W와 높이 H가 주어진다. (1 ≤ W, H ≤ 30)
다음 줄에는 묘비의 개수 G (G ≥ 0)가 주어진다.
다음 G개 줄에는 묘비의 위치를 나타내는 두 정수 X와 Y가 주어진다. (0 ≤ X < W, 0 ≤ Y < H)
다음 줄에는 귀신 구멍의 수 E (E ≥ 0)가 주어진다.
다음 E개 줄에는 귀신 구멍의 정보를 나타내는 X1, Y1, X2, Y2, T 가 주어진다.
(X1, Y1)은 귀신 구멍의 위치이고, (X2, Y2)는 그 귀신 구멍으로 들어갔을 때, 나오는 곳의 위치이다. (0 ≤ X1, X2 < W, 0 ≤ Y1, Y2 < H) (X1,Y1)과 (X2,Y2)가 같을 수도 있다.
T는 귀신 구멍에서 나오는데 걸리는 시간이다. (-10,000 ≤ T ≤ 10,000)
두 귀신 구멍이 같은 장소에 있거나, 구멍에서 나오는 지점이 묘비인 경우는 없다.
묘비와 귀신 구멍이 (0, 0)이나 (W-1, H-1)에 있는 경우는 없다.
입력의 마지막 줄에는 0 0이 주어진다.
출력
각 테스트 케이스 마다 상근이가 과거로 계속해서 돌아간다면 "Never"를 출력.
출구를 빠져나올 수 없으면 "Impossible"을 출력.
그 외의 경우에는 묘지를 빠져나오는데 가장 빠른 시간을 출력.
접근법

그리드 형태의 묘지이지만, 쉽게 그래프 형태로 바꿀 수 있음을 알 수 있다.
각 잔디가 하나의 노드가 되고, 인접한 잔디끼리 양방향 간선을 그려준 뒤, 귀신 구멍의 경우에는 구멍 입구 노드에서 출구 노드로 향하는 단방향 간선을 그려주면 된다.
묘비의 경우 갈 수 있는 방법이 없으므로 무시하면 된다.

인접한 잔디 사이의 간선의 cost는 1이고, 귀신 구멍의 간선의 cost는 입력에 따라 다르다.
아무튼 그래프 형태로 바꾸기만 하면, 음수 간선이 존재할 수 있고 (귀신 구멍), 음수 간선 사이클이 존재할 수 있는 (상근이가 영원히 과거로 되돌아 갈 수 있는) 경우에서의 최단 경로 찾기 문제임을 쉽게 알 수 있다.
즉 벨만-포드 알고리즘을 적용해주기만 하면 끝.
벨만-포드 알고리즘을 적용하기 위해서는 edge list가 필요하기 때문에, 주어진 묘지 형태에서 edge만 뽑아내면 되는데, 이 부분에서 생각해야 할 부분이 몇개 있다.
- 인접한 동서남북의 잔디로는 자유롭게 이용 가능하다. 즉 잔디 사이의 간선은 양방향 간선이다.
- 귀신 구멍이 있는 칸으로 가면 반드시 귀신 구멍의 출구로 나온다. 즉 귀신 구멍을 무시하고 지나갈 수 없다. 다시 말하면, 귀신 구멍이 있는 칸에서 인접한 칸에 대한 edge를 list에 추가하면 안된다.
- 출구에 도착하면 바로 탈출한다고 했으므로, edge를 뽑아낼 때 출구에서 인접한 칸으로 이동하는 edge는 추가하면 안된다.
이 3가지 경우를 고려하며 edge list를 뽑아낸 뒤, 벨만-포드 알고리즘을 그대~로 적용만 해주면 풀린다.
edge list를 만드는 함수
static void add_edges()
{
int[] mr = {-1, 1, 0 ,0};
int[] mc = {0, 0, -1, 1};
for (int i = 0; i < H; i ++)
{
for (int j = 0; j < W; j++)
{
//묘비 or 귀신구멍 or 출구에 대해서는 인접한 칸에 대한 간선 추가하지 않음
if (map[i][j] != GRASS)
continue;
//모든 잔디에서 인접한 칸으로 이동 가능하면 간선 추가
for (int k = 0; k < 4; k++)
{
int tr = i + mr[k];
int tc = j + mc[k];
if (can_move_to(tr, tc))
edges.add(new Edge(new Point(i, j), new Point(tr, tc), 1));
}
}
}
}
벨만-포드 알고리즘으로 답을 구하는 함수
static void get_cost_bf()
{
//벨만 포드 알고리즘에서 cost를 기록할 배열
cost = new long[H][W];
for (int i = 0; i < H; i ++)
for (int j = 0; j < W; j++)
cost[i][j] = INF; //전부 INF로 초기화
//출발점의 cost는 0으로 초기화
cost[0][0] = 0;
//묘비를 제외한 칸 개수. 즉 그래프의 전체 노드 개수를 의미함.
int V = W * H - G;
//V-1번 edge list를 선회
for (int i = 0; i < V - 1; i++)
{
for (Edge e : edges)
{
Point start = e.start;
Point end = e.end;
//start가 귀신 구멍인데 cost가 음수인 경우
//start의 cost가 INF이면 아직 start에 도달한적이 한번도 없는데
//end의 cost가 INF인 경우 end의 cost가 업데이트 되는 경우가 생김
//그 것을 막기 위해 조건을 걸어둠
if (cost[start.row][start.col] == INF)
continue;
//cost 업데이트
cost[end.row][end.col] =
Math.min(cost[end.row][end.col], cost[start.row][start.col] + e.ost);
}
}
//한번 더 cost를 업데이트함
//바뀌는게 있다는 것은 음수 싸이클이 존재한다는 뜻
for (Edge e : edges)
{
Point start = e.start;
Point end = e.end;
if (cost[start.row][start.col] == INF)
continue;
if (cost[end.row][end.col] > cost[start.row][start.col] + e.cost)
{
result.add("Never");
return;
}
}
//출구에 도달하지 못한 경우
if (cost[H - 1][W - 1] == INF)
result.add("Impossible");
else
result.add(Long.toString(cost[H - 1][W - 1]));
}
시간 복잡도
edge list를 뽑는 경우에는 묘지를 한번만 순회하면 되므로 W * H
벨만-포드 알고리즘의 경우 O(VE)인데
이 문제에서 V = W * H - G, E는 입력에 따라 달라진다.
즉 O((W * H - G)E) 인데 W와 H가 크지 않으므로 제한 시간 내에 풀 수 있다.
공간 복잡도
W와 H가 크지 않으므로 신경 안써도 된다.
풀면서 놓쳤던 점
위에서 언급했던
- 인접한 동서남북의 잔디로는 자유롭게 이용 가능하다. 즉 잔디 사이의 간선은 양방향 간선이다.
- 귀신 구멍이 있는 칸으로 가면 반드시 귀신 구멍의 출구로 나온다. 즉 귀신 구멍을 무시하고 지나갈 수 없다. 다시 말하면, 귀신 구멍이 있는 칸에서 인접한 칸에 대한 edge를 list에 추가하면 안된다.
- 출구에 도착하면 바로 탈출한다고 했으므로, edge를 뽑아낼 때 출구에서 인접한 칸으로 이동하는 edge는 추가하면 안된다.
이 3가지를 놓쳤었고,
묘지를 탈출하지 못하는 경우와 영원히 과거로 돌아가지 못하는 경우를 애매하게 구분했어서 몇번 더 틀렸다.
V - 1번 반복을 했을 때 출구에 도달하지 못했으면 그냥 탈출하지 못하는 경우로 처리했는데, 이 때 음수 싸이클이 존재하는 경우가 있어서 이런 경우는 영원히 과거로 가는 경우 처리를 해야했다.
이 문제에서 얻어갈 것
벨만-포드 알고리즘의 응용
그래프가 아닌 입력을 그래프 형태로 바꾸는 방법
코드
import java.util.Scanner;
import java.util.LinkedList;
public class Main
{
static int W, H, G, E;
static int[][] map;
static long[][] cost;
static LinkedList<Edge> edges;
static LinkedList<String> result;
static final int GRASS = 0;
static final int GRAVE = 1;
static final int HOLE = 2;
static final int EXIT = 3;
static final long INF = Integer.MAX_VALUE;
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
result = new LinkedList<String>();
while (true)
{
W = sc.nextInt();
H = sc.nextInt();
if (W == 0 && H == 0)
break;
//초깃값 0 은 GRASS를 의미
map = new int[H][W];
//출구 표시
map[H - 1][W - 1] = EXIT;
G = sc.nextInt();
//묘비 입력 받음
int row, col;
for (int i = 0; i < G; i++)
{
col = sc.nextInt();
row = sc.nextInt();
map[row][col] = GRAVE;
}
E = sc.nextInt();
//벨만 포드에 쓰일 edge list
edges = new LinkedList<Edge>();
//귀신 구멍을 입력받는 동시에 귀신 구멍 간선 추가
int row1, col1, row2, col2, t;
for (int i = 0; i < E; i++)
{
col1 = sc.nextInt();
row1 = sc.nextInt();
col2 = sc.nextInt();
row2 = sc.nextInt();
t = sc.nextInt();
map[row1][col1] = HOLE;
edges.add(new Edge(new Point(row1, col1), new Point(row2, col2), t));
}
//edge list에 edge를 마저 추가
add_edges();
//벨만포드 적용
get_cost_bf();
}
for (String s : result)
System.out.println(s);
}
static void get_cost_bf()
{
//벨만 포드 알고리즘에서 cost를 기록할 배열
cost = new long[H][W];
for (int i = 0; i < H; i ++)
for (int j = 0; j < W; j++)
cost[i][j] = INF; //전부 INF로 초기화
//출발점의 cost는 0으로 초기화
cost[0][0] = 0;
//묘비를 제외한 칸 개수. 즉 그래프의 전체 노드 개수를 의미함.
int V = W * H - G;
//V-1번 edge list를 선회
for (int i = 0; i < V - 1; i++)
{
for (Edge e : edges)
{
Point start = e.start;
Point end = e.end;
//start가 귀신 구멍인데 cost가 음수인 경우
//start의 cost가 INF이면 아직 start에 도달한적이 한번도 없는데
//end의 cost가 INF인 경우 end의 cost가 업데이트 되는 경우가 생김
//그 것을 막기 위해 조건을 걸어둠
if (cost[start.row][start.col] == INF)
continue;
//cost 업데이트
cost[end.row][end.col] =
Math.min(cost[end.row][end.col], cost[start.row][start.col] + e.cost);
}
}
//한번 더 cost를 업데이트함
//바뀌는게 있다는 것은 음수 싸이클이 존재한다는 뜻
for (Edge e : edges)
{
Point start = e.start;
Point end = e.end;
if (cost[start.row][start.col] == INF)
continue;
if (cost[end.row][end.col] > cost[start.row][start.col] + e.cost)
{
result.add("Never");
return;
}
}
//출구에 도달하지 못한 경우
if (cost[H - 1][W - 1] == INF)
result.add("Impossible");
else
result.add(Long.toString(cost[H - 1][W - 1]));
}
static void add_edges()
{
int[] mr = {-1, 1, 0 ,0};
int[] mc = {0, 0, -1, 1};
for (int i = 0; i < H; i ++)
{
for (int j = 0; j < W; j++)
{
//묘비 or 귀신구멍 or 출구에 대해서는 인접한 칸에 대한 간선 추가하지 않음
if (map[i][j] != GRASS)
continue;
//모든 잔디에서 인접한 칸으로 이동 가능하면 간선 추가
for (int k = 0; k < 4; k++)
{
int tr = i + mr[k];
int tc = j + mc[k];
if (can_move_to(tr, tc))
edges.add(new Edge(new Point(i, j), new Point(tr, tc), 1));
}
}
}
}
static boolean can_move_to(int row, int col)
{
return (row >= 0 && row < H && col >= 0 && col < W && map[row][col] != GRAVE);
}
}
class Point
{
int row;
int col;
public Point(int row, int col)
{
this.row = row;
this.col = col;
}
}
class Edge
{
Point start;
Point end;
int cost;
public Edge(Point start, Point end, int cost)
{
this.start = start;
this.end = end;
this.cost = cost;
}
}'Algorithm' 카테고리의 다른 글
| [백준] 유럽여행(1185) Java (0) | 2021.08.29 |
|---|---|
| [야매 알고리즘] Kruskal 알고리즘 (MST 찾기), 백준 1197 최소 스패닝 트리 (0) | 2021.08.26 |
| [야매 알고리즘] Disjoint-set(Union-find) (0) | 2021.08.24 |
| [백준] 공장(7578) Java (0) | 2021.08.24 |
| [백준] 단절선(11400) Java (0) | 2021.08.13 |




댓글